圧縮性乱流の高精度数値シミュレーションに関する研究
JAXAスーパーコンピュータシステム利用成果報告(2020年4月~2021年3月)
報告書番号: R20JACA37
利用分野: JSS大学共同利用
- 責任者: 河合宗司, 東北大学大学院工学研究科 航空宇宙工学専攻
- 問い合せ先: 淺田啓幸(h.asada@tohoku.ac.jp)
- メンバ: 河合 宗司, 加茂川 諒, 淺田 啓幸, 粟飯原 あや
事業概要
壁面モデルLarge-eddy simulation (LES)において,剥離・再付着を伴う高レイノルズ数の流れ場を高精度に予測するためには,乱流境界層の非平衡効果を考慮することが重要となる. しかし,従来の非平衡壁面モデルは複雑な偏微分方程式を解く必要があり,特に複雑形状周りの解析において,実装の複雑さが問題となる. そこで本研究では,新しい常微分方程式型の非平衡壁面モデルの構築および検証を行った. 具体的には,まず (a) 昨年度までに実施した通常のLES解析より得られた剥離・再付着を伴う平板乱流境界層の詳細なデータベースに基づいて,圧力勾配や移流項,渦粘性係数といった境界層の非平衡効果をモデリングし,新しい常微分方程式型の非平衡壁面モデルを構築した. そして,その構築した壁面モデルを用いて,同じ流れ場について壁面モデル解析を実施した. また,(b) より実用的な流れ場での検証として,翼型周りの流れ場について同モデルを用いた壁面モデルLES解析を実施した. その結果,その新しいモデルを用いた壁面モデルLESは,参照解とした通常のLESの結果と比較して,壁面摩擦係数や平均主流方向速度について良い予測精度を示した.
参照URL
http://www.klab.mech.tohoku.ac.jp/index_jpn.html 参照.
JAXAスーパーコンピュータを使用する理由と利点
本研究では, 新しく構築した壁面モデルLESの検証計算を実施する. 壁面モデルLESは3次元の非定常計算であるため, 並列計算は必須である. また, 新しい壁面モデルの提案のためにはパラメータ等を変化させて複数ケースの計算を行う必要がある. そのため, JAXAスパコン利用による大規模な並列計算の資源が不可欠と判断し, 申請を行った.
今年度の成果
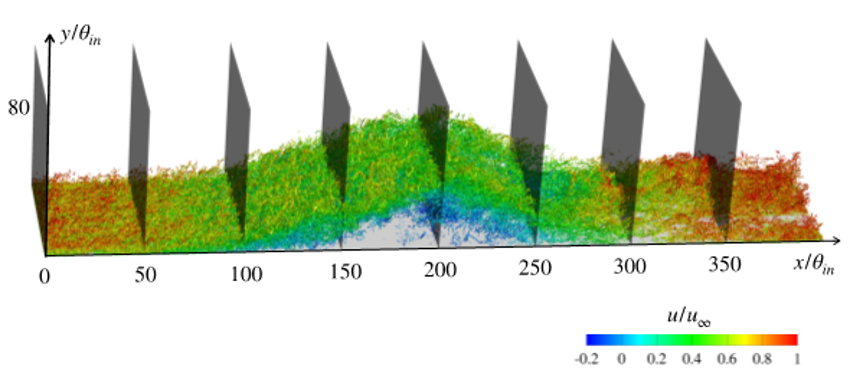
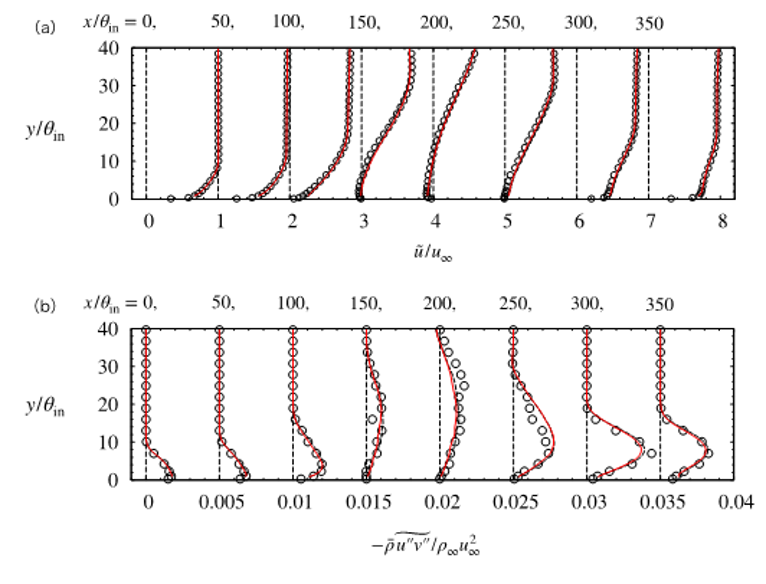
(a)昨年度までに実施した通常のLES解析より得られた剥離・再付着を伴う平板乱流境界層の詳細なデータベースに基づいて, 常微分方程式型の非平衡壁面モデルを構築した. 具体的には, 壁面モデルのマッチング高さの物理量を用いて表現できる形で, 境界層内層の圧力勾配項および移流項をモデリングした. また, せん断応力のバランスを考慮し, 渦粘性係数のモデリングを圧力勾配項や移流項とコンシステントな形に修正した. 提案モデルは常微分方程式型であり, 従来の偏微分方程式型の非平衡壁面モデルに比べて, 実装が容易という利点がある. さらに, 提案壁面モデルを用いて, 参照した剥離流れの壁面モデルLES解析(ODE-NEQWM)を実施し, 既に計算していた従来の偏微分方程式型の壁面モデルを用いた壁面モデルLES解析(PDE-NEQWM)および通常のLESの結果と比較した. 今回構築したODE-NEQWMは, 平均主流方向速度およびレイノルズせん断応力について, 比較対象としたLESや従来のPDE-NEQWMと良い一致を示している. この結果は, 偏微分方程式を解かなくても, 今回構築した常微分方程式型を解くだけで, 剥離・再付着を伴う非平衡な流れ場を高精度に予測できる可能性を示唆している.
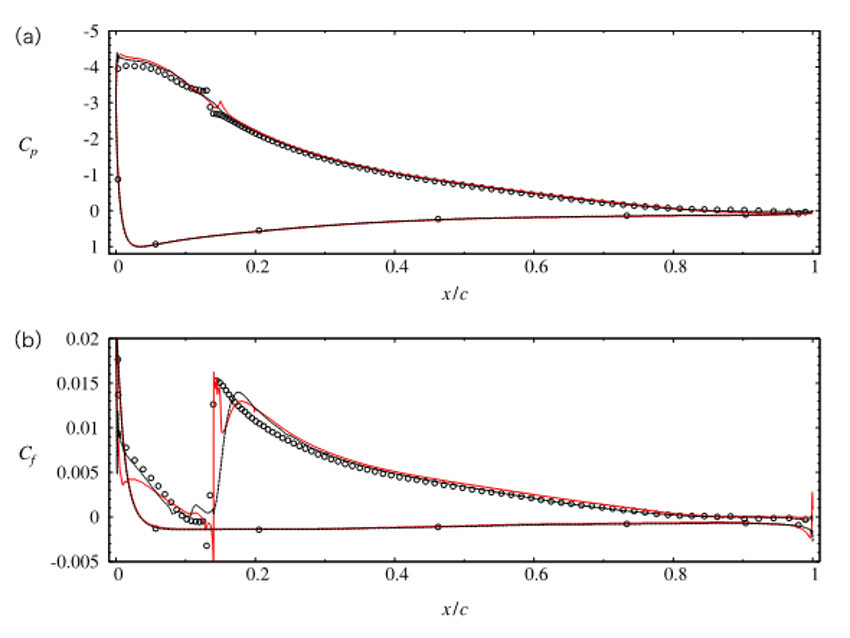
(b)より実用的な問題に近い流れ場で検証するために, 失速角付近の条件下における翼型周りの流れに対して, (a) で構築した壁面モデルを用いた壁面モデルLES解析(ODE-NEQWM)を実施した. 計算対象は先行研究(通常のLES, Asada & Kawai, PoF (2018); PDE-NEQWM, Tamaki, Fukushima, Kuya, & Kawai, PRF (2020))と同様に, A-airfoilの失速点付近(迎角13.3度)の流れ場であり, 翼弦長ベースのレイノルズ数が2.1×10^6, 一様流マッハ数が0.15である. 今回構築したODE-NEQWMは, 壁面圧力係数および壁面摩擦係数について, 比較対象とした通常のLESや従来のPDE-NEQWMと概ね良い一致を示している. なお, 翼前縁での壁面摩擦係数がLESとODE-NEQWMで若干異なる現象については, 前縁付近の非常に薄い境界層内に十分な格子点が配置されていないことが影響しており, 構築したODE-NEQWM自体の直接の問題ではないと考えられる. この点を除くと, 提案壁面モデルを用いることで, 実問題に近い翼型周りの流れ場もロバストかつ良い精度で予測できることが示された.
図1: 剥離・再付着を伴う平板乱流境界層の概略図
図2: 剥離・再付着流れの各主流方向位置における主流方向速度分布およびレイノルズせん断応力分布(丸:通常のLES, 赤実線:提案壁面モデルLES(ODE-NEQWM)黒破線:従来の壁面モデルLES(PDE-NEQWM))
図3: 翼型周りの流れ場の概略図
図4: 壁面圧力係数および壁面摩擦係数の比較(丸:通常のLES, 赤実線:提案壁面モデルLES(ODE-NEQWM)黒破線:従来の壁面モデルLES(PDE-NEQWM))
成果の公表
-口頭発表
(1)加茂川諒, 玉置義治, 河合宗司, 「剥離乱流境界層LESにおける常微分方程式型非平衡壁面モデルの提案」, 第34回数値流体力学シンポジウム, オンライン, 2020年12月
JSS利用状況
計算情報
- プロセス並列手法: MPI
- スレッド並列手法: OpenMP
- プロセス並列数: 416
- 1ケースあたりの経過時間: 200 時間
JSS2利用量
総資源に占める利用割合※1(%): 0.15
内訳
JSS2のシステム構成や主要な仕様は、JSS2のシステム構成をご覧下さい。
| 計算システム名 | コア時間(コア・h) | 資源の利用割合※2(%) |
|---|---|---|
| SORA-MA | 903,245.69 | 0.17 |
| SORA-PP | 0.00 | 0.00 |
| SORA-LM | 0.00 | 0.00 |
| SORA-TPP | 0.00 | 0.00 |
| ファイルシステム名 | ストレージ割当量(GiB) | 資源の利用割合※2(%) |
|---|---|---|
| /home | 22.32 | 0.02 |
| /data | 3,522.01 | 0.07 |
| /ltmp | 4,572.09 | 0.39 |
| アーカイバシステム名 | 利用量(TiB) | 資源の利用割合※2(%) | J-SPACE | 0.00 | 0.00 |
|---|
※1 総資源に占める利用割合:3つの資源(計算, ファイルシステム, アーカイバ)の利用割合の加重平均.
※2 資源の利用割合:対象資源一年間の総利用量に対する利用割合.
JSS3利用量
総資源に占める利用割合※1(%): 0.01
内訳
JSS3のシステム構成や主要な仕様は、JSS3のシステム構成をご覧下さい。
| 計算システム名 | コア時間(コア・h) | 資源の利用割合※2(%) |
|---|---|---|
| TOKI-SORA | 0.00 | 0.00 |
| TOKI-RURI | 0.00 | 0.00 |
| TOKI-TRURI | 0.00 | 0.00 |
| ファイルシステム名 | ストレージ割当量(GiB) | 資源の利用割合※2(%) |
|---|---|---|
| /home | 22.52 | 0.02 |
| /data | 3,523.93 | 0.06 |
| /ssd | 225.17 | 0.12 |
| アーカイバシステム名 | 利用量(TiB) | 資源の利用割合※2(%) | J-SPACE | 0.00 | 0.00 |
|---|
※1 総資源に占める利用割合:3つの資源(計算, ファイルシステム, アーカイバ)の利用割合の加重平均.
※2 資源の利用割合:対象資源一年間の総利用量に対する利用割合.
JAXAスーパーコンピュータシステム利用成果報告(2020年4月~2021年3月)
ここは、サイドバー・エリアの先頭です。