圧縮性乱流の高精度数値シミュレーションに関する研究
JAXAスーパーコンピュータシステム利用成果報告(2019年4月~2020年3月)
報告書番号: R19JACA37
利用分野: JSS2大学共同利用
- 責任者: 河合宗司, 東北大学大学院工学研究科 航空宇宙工学専攻
- 問い合せ先: 加茂川諒(kamogawa@klab.mech.tohoku.ac.jp)
- メンバ: 河合 宗司, 石塚 沙也子, 加茂川 諒
事業概要
本研究では, (a)壁面モデルLES(wall-modeled LES:WMLES)の乱流生成メカニズム, および, (b)圧力勾配に起因する剥離・再付着を伴う複雑な流れに対するWMLESの予測精度を明らかにするために, 壁面まで解像する通常の大規模LES(wall-resolved LES:WRLES)およびWMLESを実施した. その結果, WMLESでは, 壁面近傍に現れる格子スケールの対の渦構造が擬似的なストリーク構造の役割を果たし, 乱流生成に寄与していることを明らかにした. また, 圧力勾配に起因する剥離・再付着を伴う乱流境界層において, WMLESとWRLESの結果を比較すると, 壁面剪断応力に若干の誤差は見られるものの, WMLESが平均主流方向速度やレイノルズ剪断応力について良い予測精度を示すことを明らかにした.
参照URL
なし
JAXAスーパーコンピュータを使用する理由と利点
本研究では, WMLESに加えて, その検証用データベースとしての高精度・大規模LES解析が重要な役割を果たすため, LES解析の実施が必須となる. 通常の大規模LES解析では, 内層乱流まで解像する必要があるために, 高い計算コストを要する. そのため, JSS2利用による大規模並列計算が不可欠である.
今年度の成果
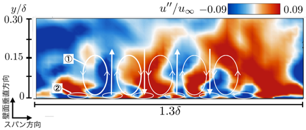
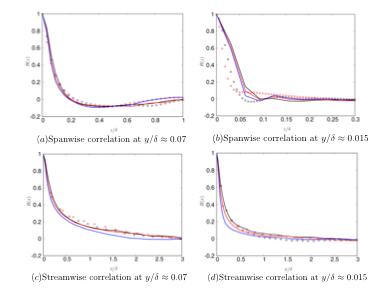
(a) 平板乱流境界層に対して通常の内層乱流まで解像するWRLESとWMLESを用いた解析を行い, 乱流統計量に加え, 瞬時の流れ場や相関係数を比較することでWMLESの乱流生成メカニズムに関する解析を実施した. 用いたレイノルズ数条件は【Re】_τ≈740,1400,8500であり, そのうち初めの2条件はWRLESが実施可能な比較的低いレイノルズ数と中程度のレイノルズ数, 三つ目は計算コストの観点からWRLESが困難であり, 今後WMLESの適用が期待される高レイノルズ数となっている. WRLESは初めの2つのレイノルズ数条件で, WMLESは全3条件で解析を実施した. また, 一様流マッハ数はいずれのレイノルズ数においてもM_∞=2.28とした. 図1は【Re】_τ≈1400おけるWMLESの主流方向速度変動量の瞬時場である. WMLESの流れ場には壁面付近に高速・低速の速度変動成分がスパン方向に交互に並んだ対の渦構造が見られる. またその構造は, 壁面ごく近傍の小さい構造およびその上方の比較的大きな構造の二層構造になることが分かった. 図2はy/δ≈0.07,0.015における主流方向速度変動量のスパン方向および主流方向自己相関係数である. 図1における壁面ごく近傍の小さい渦構造の上方に形成される渦構造①に対応するy/δ≈0.07位置の自己相関係数を見ると, WMLESはスパン方向, 流れ方向の主要な長さスケールをWRLESと同程度に捉えていることが分かった(図2 (a), (c)). 一方, 図1の壁面ごく近傍の渦構造②に対応するy/δ≈0.015では, スパン方向の長さスケールをWRLESと比較して大きく予測している(図2 (b)). この傾向は全てのレイノルズ数で同様である. またこの壁面ごく近傍の渦構造の長さスケールは, 本研究で使用する6次精度コンパクト差分法で捉えることが可能な格子6点ほどのスケールであり, 物理的なスケールの現象ではなく, 計算手法と格子スケールで決まるのスケールの現象であることが明らかになった. また一方で, この壁面ごく近傍の渦構造②は, 流れ方向にはWRLESと同程度のスケールを持っている(図2 (d)). 以上の結果より, WMLESでは壁面近傍に現れる格子スケールの対の渦構造が擬似的なストリーク構造の役割を果たし, レイノルズ応力の発生および正しい外層乱流の予測につながっていると考えられる.
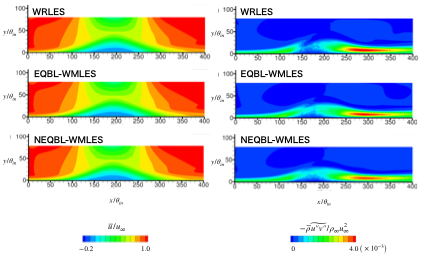
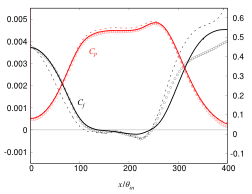
(b) 圧力勾配に起因する剥離・再付着現象を伴う乱流境界層に対して, 平衡および非平衡壁面モデルLESを実施し, 得られた乱流統計量について, WRLESデータベースと比較することで考察を行った. なお, 比較対象とした高精度WRLESデータベースは, すでに我々の研究グループで構築していたものを用いた. 流れ場条件は, 現状, WRLESが実施できる最大のレイノルズ数条件である【Re】_θ=2000, M_∞=0.2 である. 図3は平均主流方向速度およびレイノルズ剪断応力, 図4は壁面摩擦係数および壁面圧力係数を示している. 平衡および非平衡どちらの壁面モデルLESも, 平均主流方向速度およびレイノルズ剪断応力について全体的に大差は無く, 比較対象のWRLESと非常に良い一致を示している. 一方, 壁面モデルで予測する壁面剪断応力の値については, どちらの壁面モデルにおいても差異が見られる. このことは, 圧力勾配などに起因する外層での流体現象が流れ場全体に大きく影響する場合, 壁面モデルで与えられる壁面剪断応力が若干ずれていても, 外層をモデル化せずに計算しているWMLESが良い予測精度を示すことを示唆していると考えられる. 今後は壁面剪断応力と流れ場全体の関係についてより詳細に調べるとともに, 特に誤差の大きかった再付着後における壁面モデルの改善に向けた研究を行う予定である.
成果の公表
-口頭発表
石塚沙也子, 河合宗司, “壁面モデルLESにおける乱流生成機構と乱流構造, “第33回数値流体力学シンポジウム, 札幌市, 北海道, 2019年11月.
JSS2利用状況
計算情報
- プロセス並列手法: MPI
- スレッド並列手法: OpenMP
- プロセス並列数: 15 – 1930
- 1ケースあたりの経過時間: 4000000000 時間
利用量
総資源に占める利用割合※1(%): 0.02
内訳
JSS2のシステム構成や主要な仕様は、JSS2のシステム構成をご覧下さい。
| 計算システム名 | コア時間(コア・h) | 資源の利用割合※2(%) |
|---|---|---|
| SORA-MA | 152,565.24 | 0.02 |
| SORA-PP | 0.00 | 0.00 |
| SORA-LM | 0.00 | 0.00 |
| SORA-TPP | 0.00 | 0.00 |
| ファイルシステム名 | ストレージ割当量(GiB) | 資源の利用割合※2(%) |
|---|---|---|
| /home | 13.67 | 0.01 |
| /data | 4,241.31 | 0.07 |
| /ltmp | 2,799.48 | 0.24 |
| アーカイバシステム名 | 利用量(TiB) | 資源の利用割合※2(%) |
|---|---|---|
| J-SPACE | 0.00 | 0.00 |
※1 総資源に占める利用割合:3つの資源(計算, ファイルシステム, アーカイバ)の利用割合の加重平均.
※2 資源の利用割合:対象資源一年間の総利用量に対する利用割合.
JAXAスーパーコンピュータシステム利用成果報告(2019年4月~2020年3月)